Who Else Wants Info About Which Axis Is Y 4 Parallel To
Draw A Line Parallel To Y Axis At Distance Of 4 Units From The Origin
Unraveling the Mystery
1. What does Y = 4 actually mean?
Alright, let's dive into this. You've got "Y = 4," and you're wondering what it's all about, especially in terms of axes and parallels. Think of it as a simple instruction on a map. It's telling you exactly where to find something. In this case, it's a line, not buried treasure, but equally rewarding once you get it.
Imagine your standard graph, the one you probably doodled on in math class (dont worry, we all did it). You've got the horizontal axis, usually called the x-axis, and the vertical axis, the trusty y-axis. The equation Y = 4 isn't some cryptic code; it's simply saying that for every single point on this line, the y-coordinate will always, without fail, be 4. No matter what the x-value is, the y-value stays put at 4.
So, Picture this: you start plotting points. (0, 4), (1, 4), (-1, 4), (100, 4), (-50, 4). See the pattern? Each point has a y-coordinate of 4. When you connect these points, you get a straight line. And here's the magic trick: this line runs perfectly horizontally across your graph.
Therefore, to put it simply, Y = 4 defines a horizontal line. Its like a perfectly flat road stretching infinitely in both directions, always at a height of 4 units above (or below, depending on where you set your zero) the x-axis. Keep that image in your head, and you'll never forget it.

Slope Of A Line Parallel To X Axis And Y YouTube
The Parallel Connection
2. So, which axis is it parallel to?
Now, the pivotal question: "Which axis is Y = 4 parallel to?" Well, let's think about what "parallel" really means. Parallel lines are lines that run in the exact same direction, never intersecting, never even getting close enough to wave hello. They just keep going and going, side by side, forever.
Given that Y = 4 represents a horizontal line (as we discussed), it should become clear as day, that the line is parallel to the x-axis. The x-axis itself is a horizontal line, defined by Y = 0. So, Y = 4 is just like the x-axis but shifted up by 4 units.
Consider this analogy: Imagine train tracks. The two rails are parallel to each other. They run side by side and never meet (unless something goes horribly wrong). The line Y = 4 is one of those rails, and the x-axis is the other. They are both horizontal, both run in the same direction, and both will continue to do so for eternity (or at least as long as your graph paper lasts).
You might even consider the x-axis to be the "ground level" of your graph. The Y=4 line is just a line floating exactly 4 units above that ground level. Therefore, they are inherently parallel. The y-axis on the other hand is perpendicular to both. That's the difference to remember!

Visualizing the Line
3. Creating a mental image of this concept.
Sometimes, math concepts click better when you can visualize them. Forget the equations for a moment and picture a perfectly flat horizon. That's your x-axis. Now, imagine a tightrope walker strolling across that horizon, always at a height of 4 feet. That's your Y = 4 line.
The tightrope walker is always the same distance from the ground (the x-axis). He will never, ever intersect the ground unless he tragically falls. That constant distance is what makes the tightrope (Y = 4) parallel to the ground (x-axis).
Another image: think of the floor of a room. That's your x-axis. Now, imagine a shelf running along the wall, always exactly 4 feet above the floor. The shelf never touches the floor, and it runs perfectly alongside it. The shelf is your Y = 4 line.
These mental pictures help solidify the understanding that Y = 4 isn't just some abstract equation; it's a tangible line running parallel to the x-axis. The more you visualize it, the easier it will be to remember.

Real-World Applications (Yes, Really!)
4. Where does this show up in real life?
Okay, I know what you're thinking: "This is all well and good, but when am I ever going to use this in real life?" Well, believe it or not, the concept of parallel lines and coordinate systems pops up in more places than you might think.
Consider GPS navigation. GPS uses coordinate systems to pinpoint your location on Earth. While it's a bit more complex than a simple x-y graph (we're talking latitude, longitude, and altitude), the underlying principle is the same. Imagine you're flying an airplane at a constant altitude of 4,000 feet. Your flight path, if projected onto a 2D map, might resemble a line parallel to a certain axis (depending on your direction).
Another example can be found in construction. When builders are laying out the foundation for a building, they use levels and lasers to ensure that walls are parallel to each other and perpendicular to the ground. The lines they create are, in essence, visual representations of the x and y axes, and ensuring those lines are parallel is crucial for a stable and structurally sound building. Any lack of parallel structures causes catastrophic errors in engineering!
Even in video games, the concept of parallel lines is fundamental. Game developers use coordinate systems to define the position of objects and characters within the game world. When a character walks along a straight path, they are essentially moving along a line that could be described by a simple equation, potentially even one that runs parallel to an axis.
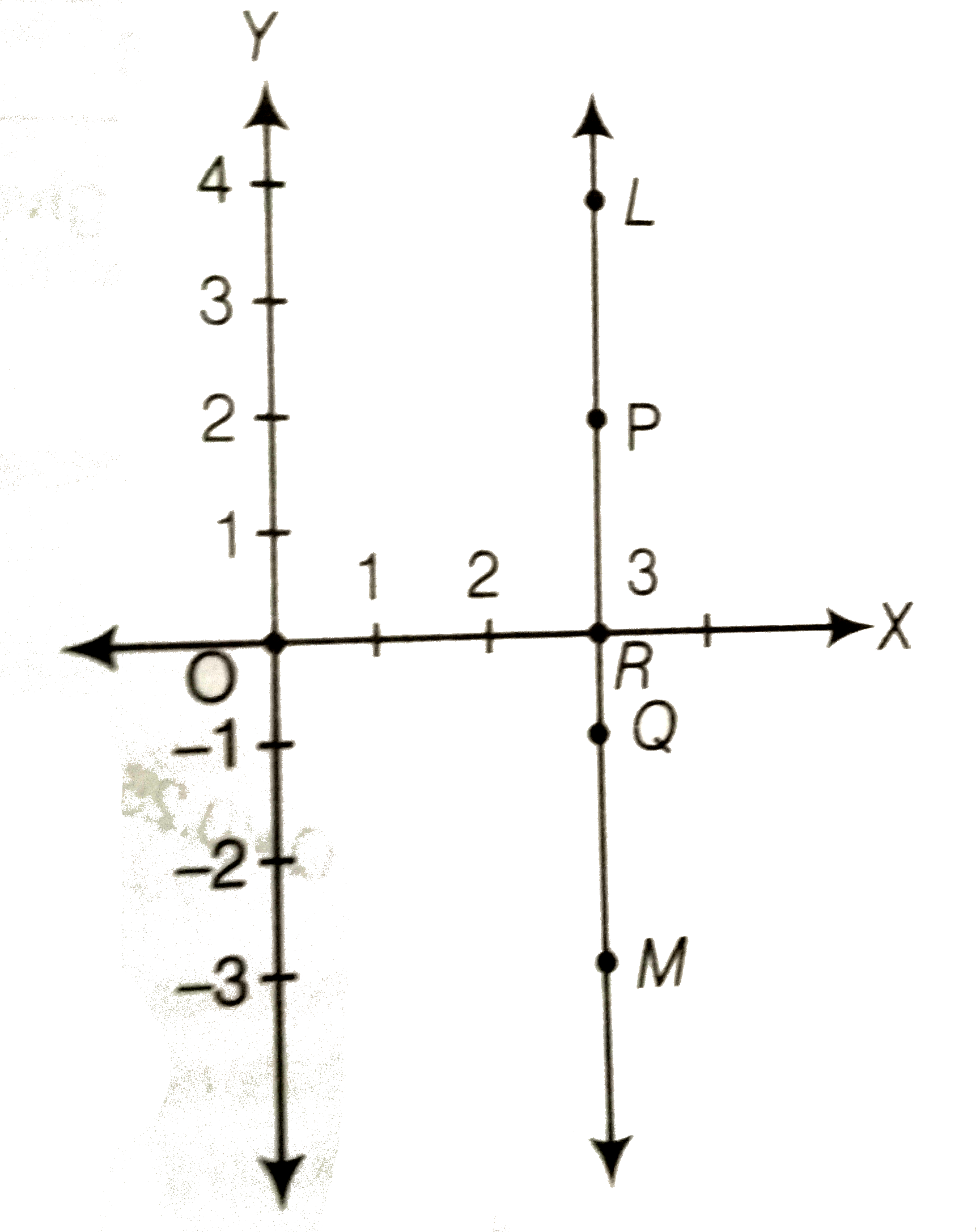
In Figure LM Is A Line Parallel To The Yaxis At Distance Of 3 Units
Frequently Asked Questions
5. Addressing common questions on this topic.
Let's tackle some of the questions that might be bubbling up in your mind.
6. Question 1
Ah, a clever question! If the equation were X = 4, then we would be dealing with a vertical line. Every point on that line would have an x-coordinate of 4, regardless of the y-coordinate. This line would run up and down, parallel to the y-axis.
7. Question 2
That's a bit of a trickier question, and it depends on your definition of "function." If you mean it in a strictly mathematical sense, then technically, no. A function must have only one output (y-value) for each input (x-value). In the equation Y=4, a single x value can be anything and Y is always 4 so it technically is a function.
8. Question 3
Now we're talking! The equation Y = X represents a line that passes through the origin (0, 0) and has a slope of 1. It's a diagonal line that cuts the x-y plane in half. It's not parallel to either the x or y axis, but it has a very special and important place in mathematics.
9. Question 4
Absolutely! In three dimensions, you have x, y, and z axes. An equation like y = 4 would then represent a plane (think of a flat sheet of paper extending infinitely) parallel to the xz-plane. It gets a bit more complicated, but the fundamental idea remains the same.
+k%2C+parallel+to+the+y-axis+e.g..jpg)